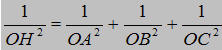Nếu c//a hoặc c//b thì do Δ ⊥ a và Δ ⊥ nên Δ ⊥ c.
Nếu c không song song với a, b, thì từ O kẻ Δ ' // Δ và kẻ c'// c. Ta chỉ cần chứng minh Δ’⊥c'
Hình 51. Minh họa cho định lý mở đầu
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Các đường thẳng a, b, c đều được xác định bởi 2 điểm và chuyển động tự do trong mặt phẳng P. O là giao điểm của a, b. Đường thẳng d’ song song với d và đi qua O. Điểm M chuyển động tự do trên d’. M’ là điểm đối xứng của M qua O. Đường thẳng c’ đi qua O và luôn song song với c. Một đường thẳng chuyển động tự do xác định bởi 2 điểm, trong đó có điểm C’ sẽ cắt a, b tại A và B.
Trên c' lấy điểm C khác O và kẻ qua C một đường thẳng cắt a và b lần lượt tại A, B khác O. Trên Δ ', về hai phía của O ta lấy hai đoạn OM = ON.
Khi đó a và b là trung trực của đoạn thẳng MN nên AM = AN, BM = BN. Suy ra tam giác MAB bằng tam giác NAB (ba cạnh tương ứng bằng nhau).Do đó góc MBC=NBC
Hai tam giác MBC và NBC có một góc và hai cạnh kề tương ứng bằng nhau nên bằng nhau, suy ra CM = CN. Tam giác CMN cân tại C nên trung tuyến CO cũng là đường cao. Vậy Δ' ⊥ c', suy ra Δ ⊥ c. Đó là điều phải chứng minh.
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì cũng vuông góc với cạnh thứ ba .
Hình 52. Minh họa cho hệ quả của định lý mở đầu
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm M chuyển động tự do trong không gian. Các điểm A, B, C chuyển động tự do trên mặt phẳng P
Δ⊥AB và Δ ⊥ AC ⇒ Δ ⊥ BC
2. Đường thẳng vuông góc với mặt phẳng
Định nghĩa: Một đường thẳng Δ gọi là vuông góc với mặt phẳng (P) nếu nó vuông góc với mọi đường thẳng của mặt phẳng đó.
Khi đó ta còn nói mp(P) vuông góc với đường Δ và kí hiệu là:
Δ ⊥ (P) hay (P)⊥ Δ
Hình 53. Định nghĩa đường thẳng vuông góc với mặt phẳng
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Mặt phẳng P được xác định bởi 3 điểm, trog đó một điểm chuyển động tự do trong không gian, hai điểm còn lại chuyển động tự do trong mặt phẳng chuẩn (mặt phẳng màu xám). Dịch chuyển các điểm này sẽ quan sát được thay đổi của P. Điểm M dịch chuyển tự do trong không gian. Đường thẳng d đi qua M và luôn vuông góc với P. Đường thẳng a chuyển động tự do trên P và được xác định bởi 2 điểm (màu đỏ, không có nhãn).
Chú ý: Theo định lí mở đầu để chứng minh Δ ⊥ (P) ta chỉ cần chứng minh Δ vuông góc với hai đường thẳng cắt nhau nào đó của mp(P).
Định lí 1: Qua một điểm O cho trước, có một mặt phẳng duy nhất vuông góc với một đường thẳng Δ cho trước.
Chứng minh: Ta kẻ Δ đi qua O và Δ'//Δ
Hình 54. Minh họa cho định lý 1.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Đường thẳng d được xác định bởi 2 điểm, điểm phía trên chuyển động tự do trong không gian, điểm phía dưới chuyển động theo phương nằm ngang. Điểm O chuyển động tự do trong không gian. Mặt phẳng R luôn đi qua O và vuông góc với d. Các đường thẳng a, b chuyển động tự do trong mặt phẳng R, mỗi đường luôn đi quan O và các định bởi một điểm thứ hai. Đường thẳng d’ luôn đi qua O là song song với d. Các mặt phẳng P, Q xác định bởi các cặp đường thẳng (d’, a) và (d’, b) tương ứng.
Lấy hai mặt phẳng (P) và (Q) phân biệt cùng đi qua Δ’;.
Gọi a, b là hai đường thẳng lần lượt nằm trên (P) và (Q) cùng đi qua O và cùng vuông góc với Δ’;. Khi đó Δ cùng vuông góc với a và b nên Δ’;⊥mp(a, b).
Vậy mp(a, b) chính là mặt phẳng đi qua O và vuông góc với Δ.
Giả sử có một mặt phẳng (R) cũng đi qua O và vuông góc với Δ thì nó phải cắt mp(P) theo một giao tuyến đi qua O và vuông góc với Δ’;, tức là giao tuyết a, tương tự (R) cũng cắt (Q) theo giao tuyết b. Vậy mp(R) phải trùng với mp(a, b).
Định lý 2: Qua một điểm O cho trước, có một và chỉ một đường thẳng vuông góc với một mặt phẳng (P) cho trước.
Chứng minh: Lấy đường thẳng a nằm trong (P), theo định lí 1 có mặt phẳng (Q) đi qua O và (Q) ⊥ a
Hình 55. Minh họa cho định lý 2.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm O chuyển động tự do trong không gian. Đường thẳng a chuyển động tự do trong mặt phẳng P xác định bởi 2 điểm tự do trong mặt phẳng này. Mặt phẳng Q đi qua O và luôn vuông góc với a. Dịch chuyển O và a để quan sát sự chuyển động của các đối tượng trên màn hình.
Trong mp(Q) ta kẻ đường thẳng Δ đi qua điểm O và vuông góc với giao tuyến b của (P) và (Q). Vì a ⊥ (Q) và Δ ⊂(Q), nên a ⊥ Δ. Như vậy Δ ⊥ (P).
Nếu qua O còn có đường thẳng Δ’; khác với Δ và vuông góc với (P) thì mp(Δ, Δ') cắt mp(P) theo giao tuyết c cùng vuông góc với Δ và Δ' đó là điều vô lí.
3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
Các tính chất sau đây học sinh có thể tự chứng minh một cách dễ dàng.
1) Cho hai đường thẳng song song. Mặt phảng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia
Hình 56. Liên hệ giữa quan hệ song song và vuông góc (1).
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Đường thẳng a đi qua 2 điểm chuyển động tự do là A, A’. Đường thẳng b đi qua điểm tự do B và song song với a. Mặt phẳng P đi qua một điểm tự do (màu đỏ) và luôn vuông góc với a, b. Dich chuyển a, b và P sẽ quan sát được sự thay đổi các đối tượng hình học trên màn hình.
a//b và (P) ⊥ a ⇒ (P) ⊥ b
2) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia
Hình 57. Liên hệ giữa quan hệ song song và vuông góc (2).
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm A chuyển động tự do trong không gian. Đường thẳng d luôn vuông góc với hai mặt phẳng P, Q. Dịch chuyển các điểm điều khiển (màu đỏ) trên P, Q để quan sát sự chuyển động của các đối tượng khác trên màn hình
(P) ⊥ (Q) và d ⊥ (P) ⇒ d ⊥ (Q)
3) Hai mặt phẳng phân biệt cùng vuông gó với một đường thẳng thì song song với nhau
Hình 58. Liên hệ giữa quan hệ song song và vuông góc (3).
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Hai điểm A, B chuyển động tự do trong không gian. Đường thẳng d đi qua A, B do vậy cũng chuyển động tự do trong không gian và luôn vuông góc với hai mặt phẳng P, Q.
(P) ⊥ d và (Q) ⊥ d và (P) ≠ (Q) ⇒ (P)// (Q)
4) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
Hình 59. Liên hệ giữa quan hệ song song và vuông góc (4).
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Mặt phẳng P xác định bởi 3 điểm X, Y, Z chuyển động tự do trong không gian. Hai đường thẳng a, b đi qua A, B và luôn vuông góc với P. Dịch chuyển A, B và các điểm X, Y, Z để quan sát
a ⊥ (P) và b ⊥ (P) và a ≠ b ⇒ a//b
5) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng thì chúng song song với nhau
Hình 60. Liên hệ giữa quan hệ song song và vuông góc (5).
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Đường thẳng b có thể dịch chuyển bất kỳ tròn không gian và được xác định bởi 2 điểm B, B’ chuyển động tự do trong không gian. Điểm A chuyển động tự do trong không gian. Điểm A’ chuyển động sao cho đường thẳng a luôn vuông góc với b. Mặt phẳng P đi qua một điểm điều khiển (màu đỏ) và luôn vuông góc với b. Dịch chuyển B, B’, A, A’ và P để quan sát sự chuyển động trên màn hình.
a ⊄ (P) và a ⊥ b và (P) ⊥ b
4. Ví dụ
Cho tứ diện SABC có ABC là tam giác vuông tại B và SA vuông góc với mặt phẳng (ABC).
a) Chứng minh BC ⊥ (SAB)
b) Gọi AH là đường cao của tam giác SAB. Chứng minh AH ⊥ SC.
Giải.
a) Ta có SA ⊥ (ABC) nên SA ⊥ BC
Hình 61. Minh họa cho ví dụ
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Trong hình vẽ trên SA luôn vuông góc với mặt phẳng chứa tam giác ABC. SB vuông góc với BC. AH là đường cao của tam giác SAB
BC ⊥ SA và BC ⊥ AB ⇒ BC ⊥ (SAB)
b) Ta có BC ⊥ (SAB) và AH ⊂(SAB). Vậy BC ⊥ AH.
AH ⊥ BC và AH ⊥ SB ⇒ AH ⊥ SC
5. Phép chiếu vuông góc.
Định nghĩa: Phép chiếu song song lên mặt phẳng (P) theo phương l sẽ gọi tiếp là phép chiếu vuông góc lên mp (P) nếu l⊥mp(P). Cũng có thể gọi nó đơn giản là phép chiếu lên mp(P)
Hình 62. Phép chiếu vuông góc
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Các điểm M, N, K chuyển động tự do trong không gian. M’, N’, K’ là hình chiếu vuông góc của các điểm M, N, K lên mặt phẳng P.
Nếu (H') là hình chiếu vuông góc của hình (H) lên mp(p) thì ta cũng nói gọn : (H') là hình chiếu của (H) lên (P).
Định lí 3: (Định lí ba đường vuông góc)
Cho đường thẳng a không vuông góc với mặt phẳng P.
Một đường thẳng b năm trong mp(P) vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu của a trên mp(P).
Chứng minh: Nếu a nằm trong (P) thì hình chiếu a' của a lên (P) chính là a. Vì vậy a ⊥ b ⇔ a' ⊥ b.
Nếu a không nằm trong (P) thì ta lấy điểm A ∈ a và A ∉ (P). Gọi A' là hình chiếu của A trên mp(P), và đặt (P) ∩ (a, A') = a' ta có a' chính là hình chiếu của a trên mp(P)
Hình 63. Định lý 3 đường vuông góc
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Hai điểm A, B chuyển động tự do trong không gian. Điểm M chuyển động tự do trong mặt phẳng P. Dùng chuột dịch chuyển các điểm A, B, M để quan sát sự thay đổi của các đường thẳng a, b, a’. Các đường thẳng a, b luôn vuông góc với nhau.
Ta có AA' ⊥ (P) và b ⊂(P) nên b ⊥ AA'.
Bởi vậy nếu b ⊥ (P) và b ⊥ mp(a, A') do đó b ⊥ a'.
Đảo lại nếu b ⊥ a' thì b ⊥ mp(a, A') do đó b ⊥ a.
6. Mặt phẳng trung trực.
Định nghĩa: Mặt phẳng trung trực của một đoạn t hẳng là mặt phẳng vuông gó với đoạn thẳng đó tại trung điểm của nó.
Định lý 4. Tập hợp các điểm cách đều hai đầu của một đoạn thẳng là mặt phẳng trung trực của đoạn thẳng đó.
Chứng minh: Cho đoạn thẳng AB, (P) là mặt phẳng của trung trực của AB, nghĩa là (P) vuông góc với AB tại trung điểm O của đoạn AB
Hình 64. Mặt phẳng trung trực
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Các điểm A, B chuyển động tự do trong không gian. M chuyển động tự do trong mặt phẳng P là trung trực của đoạn thẳng AB.
Xét một điểm M bất kì trong không gian.
Nếu M ∈ (P) thì do AB ⊥ (P) nên AB ⊥ OM. Trong mp(ABM), OM là đường trung trực của AB suy ra MA = MB.
Đảo lại nếu MA = MB thì tam giác AMB cân tại M nên trung tuyến MO cũng là đường cao, vậy MO ⊥ AB suy ra MO ⊂( P) do đó M ∈( P).
7. Phép đối xứng qua một mặt phẳng.
Cho một mặt phẳng (P)
Định nghĩa: Phép đối xứng qua mặt phẳng (P) là phép cho tương ứng với mỗi điểm M trong không gian một điểm M' sao cho mp(P) là mặt phẳng trung trực của đoạn MM'
Hình 65. Phép đối xứng qua một mặt phẳng
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Điểm M chuyển động tự do trong không gian. Có thể dịch chuyển mặt phẳng P theo phương thẳng đứng bởi điểm màu đỏ. Cho điểm M hoặc P chuyển động và quan sát hoạt động của phép đổi xứng qua mặt phẳng.
Khi đó người ta còn có thể nói:
- M' là ảnh của M qua phép đối xứng qua mp(P) hoặc:
- M và M' đối xứng với nhau qua mp(P).
Trường hợp đặc biệt nếu M thuộc mp(P) thì ta quy ước M' trung với M.
Nếu có một hình H nào đó thì tập hợp các ảnh M' của tất cả các điêm M thuộc hình H sẽ làm thành một hình H’
Ta nói hình H’ là hình đối xứng của hình h qua mp(P) hoặc hai hình H và H'’ đối xứng với nhau qua mp(P)
Hình 66. Phép đối xứng qua mặt phẳng của tứ diện ABCD.
(Nếu không xem được hình ảnh 3D hãy kích chuột tại đây để xem từng hình cụ thể)
Tứ diện ABCD được xây dựng từ 4 điểm A, B, C, D chuyển động tự do trong không gian.
Các điểm A’, B’, C’, D’ là đối xứng của A, B, C, D qua mặt phẳng P. Có thể cho P chuyển động thẳng đứng bởi một điểm điều khiển (màu đỏ).
Điểm M chuyển động trên cạnh AC. M’ là đối xứng của M qua P và nằm trên cạnh A’C’.
Trên hình hiện rõ các đường thẳng vuông góc với P đi qua các đỉnh của tứ diện ABCD để dễ dàng quan sát khi dịch chuyển các điểm A, B, C, D trong không gian
Hình 66: Tứ diện A’B’C’D’ là hình đối xứng của tứ diện ABCD qua mp(P).
CÂU HỎI BÀI TẬP
1. Cho hai đường thẳng a, b và mặt phẳng (P). Các mệnh đề sau đây đúng hay sai?
a) Nếu a//(P) và b ⊥ (P) thì a⊥b
b) Nếu a//(P) và b ⊥ a thì b ⊥ (P)
c) Nếu a //( P) và b//a thì b//(P).
2. Cho tứ diện ABCD có hai mặt ABC và DBC là hai tam giác cân có chung đáy BC.
a) Chứng minh rằng BC ⊥ AB.
b) Gọi I là trung điểm BC, AH là đường cao của tam giác ADI. Chứng minh rằng AH ⊥ mp(BCD).
3. Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O. Biết tằng SA = SC, SB = SD. Chứng minh rằng.
a) SO ⊥ mp(ABCD)
b) AC ⊥ SD.
4. Cho (T) là đường tròn nằm trên mặt phẳng (P) và có tâm O. Đường thẳng vuông góc với (P) và đi qua O gọi là trục của đường tròn (T).
Chứng minh rằng quỹ tích các điểm cách đều ba đỉnh của một tam giác là trực của đường tròn ngoại tiếp tam giác đó.
5. Cho tứ diện ABCD. Chứng minh rằng nếu AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC.
6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. Kẻ OH ⊥ mp (ABCD), H nằm trên mp(ABC). Chứng minh.
a) H là trực tâm giác ABC.
b)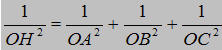
School@net
|
Tìm kiếm
Xem giỏ hàng
Khách: 6
Thành viên: 0
Tổng cộng: 6
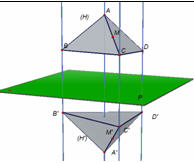1. Định lý mở đầu. 
